3.1.2 Charge triangle équilibrée
On considère maintenant une charge triangle équilibrée avec une même impédance \(Z\) entre chaque paire de phases.
Mise en équation en coordonnées usuelles
Les équations en coordonnées usuelles sont :
\begin{equation}
\begin{cases}
Z I_A = (V_A – V_B) + (V_A – V_C) = 2 V_A – V_B – V_C \\
Z I_B = (V_B – V_A) + (V_B – V_C) = 2 V_B – V_A – V_C \\
Z I_C = (V_C – V_A) + (V_C – V_B) = 2 V_C – V_A – V_B.
\end{cases}
\end{equation}
Notre composant fait intervenir deux triplets de variables triphasées, \(V_{ABC}\) et \(I_{ABC}\), qui sont ses variables de port ; il ne comporte aucune variable isolée, ni aucune variable interne. Le système compte 6 variables et trois équations indépendantes, soit trois degrés de liberté comme cela est attendu pour un composant à trois ports.
Remarque :
Les équations ne sont en fait indépendantes que si \(Z \neq 0\). Le cas \(Z = 0\) est celui du défaut triphasé franc, qui sera étudié plus tard.
La matrice comporte un bloc triphasé d’équations et aucune équation isolée. Dans l’unique bloc triphasé d’équations, les deux sous-matrices (c’est-à-dire les blocs \(A_i^j\) au sens de l’équation 2.1 sont respectivement égales à \(Z \, I_3\) pour ce qui concerne le triplet \(I_{ABC}\) et à
\begin{equation}
\begin{bmatrix}
-2 & 1 & 1 \\
1 & -2 & 1 \\
1 & 1 & -2
\end{bmatrix}
\end{equation}
pour ce qui concerne le triplet \(V_{ABC}\). La matrice possède donc la structure circulante. De plus, toutes les sous-matrices \(3 \times 3\) du problèmes vérifient \(\beta = \gamma\) au sens de la remarque 3, de sorte qu’on s’attend à ce que les systèmes direct et inverse soient identiques.
Changement de base sur les triplets de variables triphasées
On effectue le changement de variables :
\begin{equation}
\label{eq:charge-triangle-post-Fortescue}
\begin{cases}
Z (I_0 + I_d + I_i) = 3 V_d + 3 V_i \\
Z (I_0 + a^2 I_d + a I_i) = 3 a^2 V_d + 3 a V_i \\
Z (I_0 + a I_d + a^2 I_i) = 3 a V_d + 3 a^2 V_i.
\end{cases}
\end{equation}
Le problème est désormais exprimé en variables symétriques, mais la structure diagonale n’est pas encore apparue.
Changement de base sur les blocs triphasés d’équations
On applique les prémultiplications par \((1, 1,1)\), puis par \((1, a^2, a)\) et enfin par \((1, a, a^2)\), qui donnent :
\begin{equation}
\begin{cases}
I_0 = 0, \\
V_i = \frac{Z}{3} I_i, \\
V_d = \frac{Z}{3} I_d.
\end{cases}
\end{equation}
Schéma électrique symétrique
Notre charge en triangle équilibrée peut donc être vue, en composantes symétriques, comme deux impédances de même valeur \(\frac{Z}{3}\) placées respectivement dans le circuit direct entre le port \((V_N, I_N)\) et l’origine des potentiels, et dans le circuit indirect entre le port \((V_i, I_i)\) et l’origine des potentiels. Enfin, dans le circuit homopolaire, notre charge en triangle est équivalente à un fil en l’air sur le port \((V_0, I_0)\) : le courant \(I_0\) y est nul, et le potentiel \(V_0\), qui n’apparaît nulle part dans les équations, y est quelconque. La situation est représentée sur la figure ci-dessous.
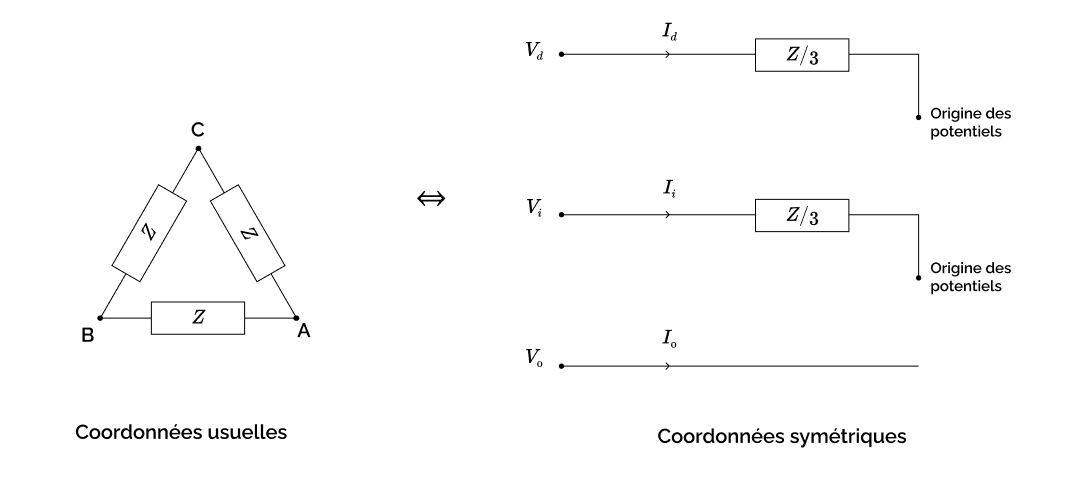
Remarque : On observe qu’une charge étoile équilibrée à neutre non-relié réalisée avec un triplet d’impédances \(Z\) d’une part, et une charge triangle équilibrée réalisée avec un triplet d’impédances \(3Z\) d’autre part, sont équivalentes : elles ont exactement le même schéma électrique symétrique. On aurait pu arriver à la même conclusion sans passer par la théorie des composantes symétriques, par exemple simplement utilisant la transformation de Kennelly.
Remarque : Nous avons démontré dans la partie 2 qu’un composant triphasé équilibré passif pouvait être représenté sous forme de trois système découplé direct, inverse et homopolaire, ne faisant respectivement intervenir que les variables directes, inverses, et homopolaires/isolées. Dans le cas d’une charge, qui ne possède qu’un seul triplet triphasé de ports, on aboutira donc dans le cas du système direct à un système linéaire ne faisant intervenir que \(V_d\) et \(I_d\), qui se ramènera nécessairement à un seul paramètre numérique que l’on pourra interpréter comme une impédance placée entre le port \((V_d, I_d)\) et l’origine des potentiels. Le même raisonnement s’applique au système inverse. Le cas du système homopolaire est un peu moins clair mais, après application du changement de variable \(I_n \longrightarrow \tilde{I}_N\), on peut penser que cela fonctionne encore et que le système homopolaire se ramènera nécessairement à une impédance placée entre les ports \((V_0, I_0)\) et \((V_N, \tilde{I}_N)\). Autrement dit, la théorie des composantes symétriques offre une manière standardisée, et minimale de décrire une charge triphasée équilibrée, sous la forme de trois « impédances symétriques » placées comme sur le schéma électrique de la charge étoile équilibrée. Ceci permet notamment de comparer facilement deux charges équilibrées qui sont structurellement différentes, comme la charge étoile à neutre non-relié et la charge triangle dans la remarque précédente, en les ramenant à une description unifiée. L’exemple des charges couplées, que nous allons bientôt traiter, nous donnera un nouvel exemple de l’intérêt de cette approche.
Modélisation de la charge triangle directement en coordonnées symétriques, sans passer par les coordonnées usuelles
A titre d’exemple, essayons une nouvelle fois d’appliquer la méthode des solutions particulières.
On cherche d’abord une solution purement directe. La loi d’Ohm sur la branche qui va de A vers B impose à \((V_d – a^2 V_d)/Z = \frac{1-a^2}{Z} V_d\) et celle sur la banche de A vers C impose à \(\frac{1-a}{Z} V_d\), tandis que la loi des noeud au sommet A du triangle impose \(I_d = \frac{2-a-a^2}{Z} V_d = \frac{3}{Z} V_d\). Il n’est pas nécessaire de refaire le travail sur B et C car les équations correspondantes seront liées à celle que nous avons déjà trouvée. L’équation directe est donc \(V_d = \frac{Z}{3} I_d\).
On cherche ensuite une solution purement inverse. La situation étant identique à celle du mode direct, on trouve instantanément \(V_i = \frac{Z}{3} I_i\).
Enfin on cherche une solution purement homopolaire et on voit que seule la solution \(I_0=0\) (avec \(V_0\) quelconque) convient.
Nous avons ainsi déterminé les équations symétriques de la charge triangle sans avoir besoin d’écrire les équations en coordonnées usuelles, et sans avoir à effectuer le moindre changement de base.
