3.1.1 Charge étoile équilibrée
Considérons une charge étoile équilibrée, avec une impédance \(Z\) sur chaque branche. Le neutre est supposé sorti.
Mise en équations en coordonnées usuelles
Les équations en coordonnées usuelles sont :
\begin{equation}
\begin{cases}
V_A – V_N = Z \, I_A \\
V_B – V_N = Z \, I_B \\
V_C – V_N = Z \, I_C \\
I_A + I_B + I_C + I_N = 0.
\end{cases}
\end{equation}
Notre problème fait intervenir deux triplets de variables triphasées, \(V_{ABC}\) et \(I_{ABC}\), ainsi que deux variables isolées \(V_N\) et \(I_N\). Toutes ces variables sont des variables de ports ; le composant ne dispose d’aucune variable interne. Le problème compte 8 variables, 4 équations indépendantes et donc 4 degrés de liberté, comme on s’y attend à un composant à 4 ports.
La matrice comporte un bloc triphasé d’équations (les trois premières) et une équation isolée (la quatrième). Dans l’unique bloc triphasé d’équations, les deux sous-matrices \(3 \times 3\) (c’est-à-dire les \(A_i^j\), avec les notations de l’équation (1)) sont respectivement : égale à la matrice identité \(I_3\) pour celle qui concerne le triplet \(V_{ABC}\), et égale à \(-Z \, I_3\) pour celle qui concerne le triplet \(I_{ABC}\) ; ces deux matrices \(3 \times 3\) sont circulantes. Dans l’unique bloc triphasé d’équations toujours, le bloc qui concerne les variables isolées est égal à \(\mathbf{1}\) pour ce qui concerne la variable \(V_N\), et il est nul pour ce qui concerne la variable \(I_N\) ; les deux colonnes sont donc des multiples de \(\mathbf{1}\). Enfin, dans l’unique équation isolée, la sous-matrice qui concerne le triplet \(V_{ABC}\) est nulle, et celle qui concerne le triplet \(I_{ABC}\) est égale à \(\mathbf{1}^\top\) ; ces deux matrices lignes sont des multiples de \(\mathbf{1}^\top\). La matrice du problème possède donc la structure circulante.
On observe également que toutes les matrices circulantes \(3 \times 3\) du problème vérifient \(\beta = \gamma \, (=0)\) au sens de cette remarque ; au vu de cette remarque , on s’attend donc à ce que les système inverse et le système direct qui apparaîtront après le double changement de bases soient identiques.
Changement de base sur les triplets de variables triphasées
Effectuons le changement de variable pour passer en coordonnées symétriques. On rappelle que ce changement ne concerne que les triplets triphasés, ici \(V_{ABC}\) et \(I_{ABC}\), et n’affecte pas les variables isolées, ici \(V_N\) et \(I_N\). Le système d’équations devient :
\begin{equation}
\begin{cases}
V_0 + V_i + V_d – V_N = Z (I_0 + I_i + I_d) \\
V_0 + a V_i + a^2 V_d – V_N = Z (I_0 + a I_i + a^2 I_d) \\
V_0 + a^2 V_i + a V_d – V_N = Z (I_0 + a^2 I_i + a I_d) \\
3 I_0 + I_N = 0.
\end{cases}
\end{equation}
Changement de base sur les blocs triphasés d’équations
Cette dernière formulation est bien « en composantes symétriques », mais elle ne fait pas encore apparaître le découplage espéré ; en effet, nous devons encore effectuer le changement de base pour les blocs triphasés d’équations. Ceci revient à prémultiplier le système linéaire par \(F^{-1}\), c’est-à-dire successivement par \((1, 1, 1)\), puis par \((1, a^2, a)\) et enfin par \((1, a, a^2)\).
Pour \((1,1,1)\), on obtient :
\begin{equation}
V_0 – V_N = Z I_0,
\end{equation}
qui est l’équation homopolaire du bloc triphasé (que nous compléterons avec l’équation isolée, \(3 I_0 + I_N = 0\), pour former le système d’équations homopolaire complet). Comme attendu, celle-ci ne fait intervenir que les variables homopolaires (ici \(V_0\) et \(I_0\)) et les variables isolées (ici \(V_N\) et \(I_N\), cette dernière n’étant pas utilisée).
Poursuivons avec \((1, a^2, a)\) pour obtenir :
\begin{equation}
V_i = Z I_i
\end{equation}
qui est l’équation inverse du bloc triphasé. Comme attendu, celle-ci ne fait intervenir que des variables inverses.
Enfin, avec \((1, a, a^2)\), on obtient :
\begin{equation}
V_d = Z I_d
\end{equation}
qui est l’équation directe du bloc triphasé et qui ne fait intervenir que des variables directes. Comme attendu, cette équation est identique à celle du système inverse.
En introduisant la variable \(\tilde{I}_N\) définie dans la section 3, les équations complètes de la charge étoile en composantes symétriques sont donc :
\begin{cases}
V_d = Z I_d \\
V_i = Z I_i \\
V_0 – V_N = Z I_0 \\
I_0 + \tilde{I}_N = 0,
\end{cases}
qui présente bien la structure découplée avec un système direct (première équation), un système inverse (deuxième équation) et un système homopolaire (troisième et quatrième équations).
Remarque : Si l’on n’avait pas effectué le changement de variable \(I_n \longrightarrow \tilde{I}_N\), on aurait dû trouver un schéma électrique équivalent aux équations
\begin{cases}
V_0 – V_N = Z I_0 \\
3 \, I_0 + I_N = 0.
\end{cases}
Schéma électrique symétrique
Autrement dit, en passant en composantes symétriques puis en cherchant à exprimer les équations obtenues comme celles d’un circuit électrique équivalent, notre charge étoile revient à trois impédances séparées, chacune de même valeur \(Z\) que sur chaque branche de la charge étoile initiale, et placées respectivement : entre le port \((V_0, I_0)\) et le port \((V_N, \tilde{I}_N)\) pour le circuit homopolaire ; entre le port \((V_i, I_i)\) et le point d’origine des potentiels pour le circuit inverse ; et entre le port \((V_d, I_d)\) et le point d’origine des potentiels pour le circuit direct. Le circuit électrique symétrique est donc celui présenté sur la figure ci-dessous.
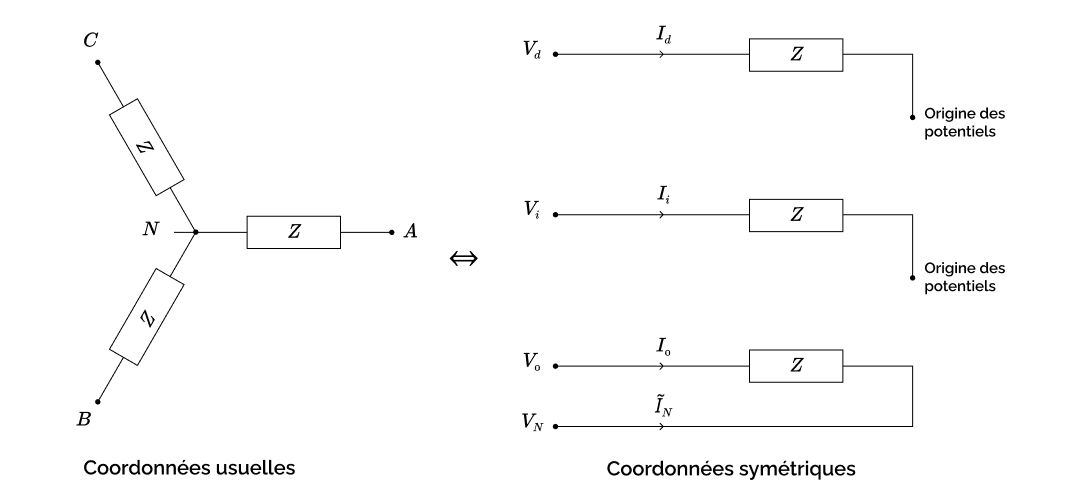
Remarque : Le schéma direct et le schéma inverse font apparaître une connexion avec l’origine des potentiels. Cette connexion devrait donc a priori apparaître dans les équations sous la forme d’une variable de courant vers l’origine des potentiels, qui serait égale à \(-I_d\) (respectivement \(-I_i\)). Le schéma que nous avons proposé ne semble donc pas équivalent aux équations symétriques. Il l’est pourtant : en effet, la variable de courant vers l’origine des potentiels est inutile dans la mesure où la loi des nœuds est supprimée au niveau de ce nœud spécial, et où la variable de courant vers l’origine n’intervient dans aucune autre équation. On peut donc la supprimer.
Cas où le point neutre de la charge n’est pas sorti
Si l’on considère que le neutre de notre charge étoile n’est pas sorti, alors on supprime l’inconnue \(I_N\). Le problème passe à 7 inconnues et toujours 4 équations, soit trois degrés de liberté, comme il convient à un composant à trois ports. L’une des quatre équations est simplement modifiée (\(3 I_0 + I_N = 0\) devient simplement \(I_0 = 0\)). Le schéma électrique symétrique est le même, à ceci près que le port \((V_0, I_0)\) est maintenant flottant et simplement relié à \(V_N\), pour traduire les équations \(I_0=0\) et \(V_0=V_N\). Le circuit électrique symétrique est donc celui présenté sur la figure 2.
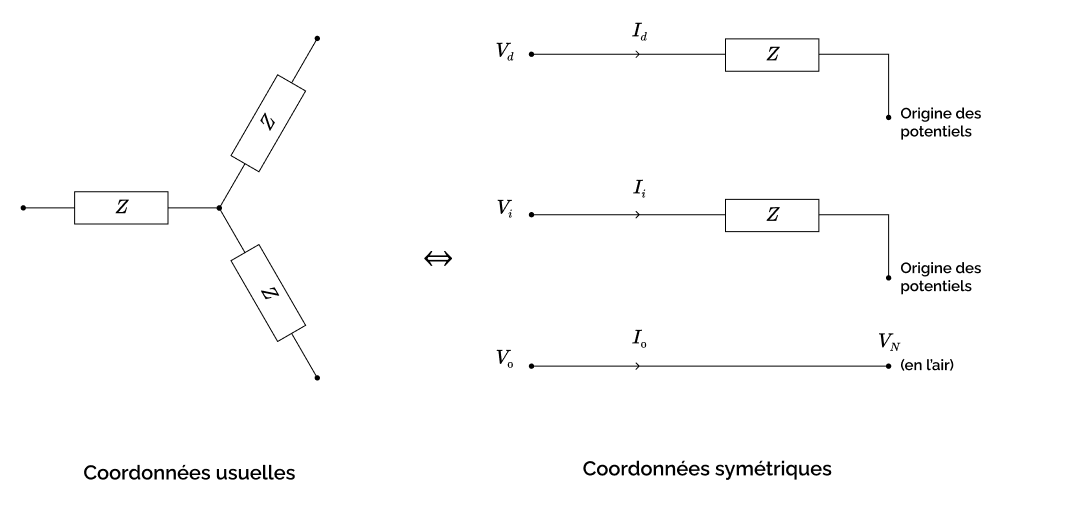 Schéma électrique usuel (à gauche) et symétrique (à droite) de la charge étoile équilibrée sans port neutre
Schéma électrique usuel (à gauche) et symétrique (à droite) de la charge étoile équilibrée sans port neutre
Modélisation de la charge étoile directement en coordonnées symétriques, sans passer par les coordonnées usuelles
Cette partie illustre la méthode qui a été présentée dans la section 2.5 et qui permet d’obtenir les équations en coordonnées symétriques en cherchant des solutions particulières purement directes, purement inverses et purement homopolaires. Le raisonnement peut être fait soit à partir des équations écrites en coordonnées usuelles, soit directement à partir du schéma électrique (usuel) sans même écrire le jeu d’équation associé ; c’est cette deuxième technique, plus rapide, que nous allons illustrer ici.
Remarque : Inversement, si l’on souhaite partir du jeu d’équations en coordonnées usuelles, il suffit de substituer aux variables usuelles leur expression en coordonnées symétriques, en tenant compte des fixations à zéro ; par exemple, lorsqu’on cherche des solutions purement directes, on substituera \(V_d\) à \(V_A\), puis \(a^2 V_d\) à \(V_B\), puis \(a V_d\) à \(V_C\), etc.
Commençons par chercher les solutions purement directes, de la forme
$$V_{ABC} = (V_d, a^2 V_d, a V_d) ,~ I_{ABC} = (I_d, a^2 I_d, a I_d), ~V_n = 0, I_N = 0.$$
On écrit la première équation que l’on aurait écrite si l’on raisonnait normalement, en coordonnées usuelles, qui est la loi d’Ohm sur la phase A. Comme \(V_N\) a été fixée à zéro, celle-ci se réduit à
$$V_d = Z \, I_d.$$
On aurait normalement écrit ensuite deux équations de loi d’Ohm sur les phases B et C, mais on ne le fait pas, car on se rend compte que celles-ci seront redondantes avec celle que nous avons déjà trouvée. Enfin, nous aurions normalement écrit pour finir la loi des nœuds dans notre composant, mais on voit tout de suite que celle-ci est ici équivalente à l’équation triviale \(0=0\) et on ne prend donc pas la peine de l’écrire. C’est fini, nous avons trouvé les équations du système direct.
On cherche ensuite des solutions purement inverses. Le raisonnement est entièrement identique et mène à l’équation
$$V_i = Z \, I_i.$$
Enfin, on cherche des solutions « purement homopolaires » ; ce qui, pour mémoire, signifie en fait des solutions dans lesquelles on conserve les variables homopolaires et les variables isolées, et où on fixe à zéro les variables directes et inverses. Pour notre charge étoile, on cherche donc une solution où \(I_0\), \(V_0\), \(I_N\) et \(V_N\) sont quelconques et où toutes les autres variables sont nulles. On reprend l’écriture de nos équations, en commençant comme ci-dessus par la loi d’Ohm sur la phase A :
$$V_0 – V_N = Z \, I_0.$$
On s’abstient ensuite d’écrire la loi d’Ohm sur les phases B et C, dont on voit facilement qu’elle sera exactement la même que sur la phase A. Enfin, on écrit la loi des nœuds :
$$3 \, I_0 + I_N = 0.$$
Nous venons d’arriver au modèle symétrique de notre composant sans jamais écrire les équations au sens usuel, et sans faire le moindre calcul de changement de base !
Remarque : Si, par erreur, on avait cherché une solution de type « \(V_0\), \(I_0\) et \(I_N\) quelconques et tout le reste nul » (c’est-à-dire si l’on avait oublié de libérer la variable \(V_N\) dans la recherche de solutions particulières purement homopolaires), on aurait quand même trouvé une famille de solutions, en l’occurrence
$$ V_0 = Z I_0 \quad \mbox{et} \quad 3 I_0 + I_N = 0. $$
Quelque chose nous aurait néanmoins permis de nous douter que nous avions commis une erreur : notre famille de solutions n’aurait été que de dimension 3 (1 pour le système direct, 1 pour le système inverse et 1 pour notre système homopolaire erroné), alors que notre composant possède 4 ports et doit donc avoir 4 degrés de liberté (c’est-à-dire une famille de solutions de dimension 4).
Sommaire
Partie 1 : Coordonnées usuelles et coordonnées symétriques
Partie 2 : Modélisation d’un composant triphasé équilibré passif général
Partie 3 : Modélisation symétrique des composants triphasés usuels
3.1.1 Charge étoile équilibrée
3.1.2 Charge triangle équilibrée
3.1.3 Cas d’une charge couplée équilibrée : le transformateur étoile-triangle avec secondaire à vide
3.2.1 Ligne équilibrée simple à trois conducteurs
3.2.2 Ligne équilibrée simple à quatre conducteurs
3.2.3 Ligne équilibrée à trois conducteurs avec couplages capacitifs entre conducteurs
3.2.4 Ligne équilibrée à quatre conducteurs avec couplages capacitifs entre conducteurs
3.2.5 Agrégation de lignes successives.
3.3 Transformateurs triphasés formés de trois transformateurs monophasés identiques
3.3.1 Transformateur étoile-étoile
3.3.2 Transformateur triangle-étoile
(travail en cours : publication prévue sur les mois de janvier à mars 2025)





