Cas d’une charge couplée équilibrée : le transformateur étoile-triangle avec secondaire à vide
On considère un transformateur étoile-triangle dont le primaire en étoile est utilisé et dont le secondaire en triangle est laissé à vide, ce qui constitue une charge couplée à 4 ports.
Remarque : Le « générateur homopolaire » est un dispositif électrotechnique standard qui ressemble beaucoup à celui qui est décrit dans cet article ; la seule différence semble être la présence d’une résistance additionnelle dans le bobinage en triangle. Ce dispositif est apparemment utilisé lorsque le plan de protection exige la mise à la terre du neutre en un certain point du réseau, et que l’on n’y dispose pas déjà naturellement d’un point neutre. Dans cette situation, le générateur homopolaire permet de créer le point neutre manquant.
On suppose que le transformateur triphasé est constitué par assemblage de trois transformateurs monophasés indépendants, ce qui nous permettra d’utiliser un modèle classique de transformateur monophasé avec une impédance transversale, dite magnétisante, au primaire, et une impédance série au secondaire.
Les trois transformateurs sont identiques, ce qui rend l’objet invariant par permutation circulaire des phases. Leur rapport de transformation, qui n’a pas grande importance dans le cas présent, est supposé égal à 1.
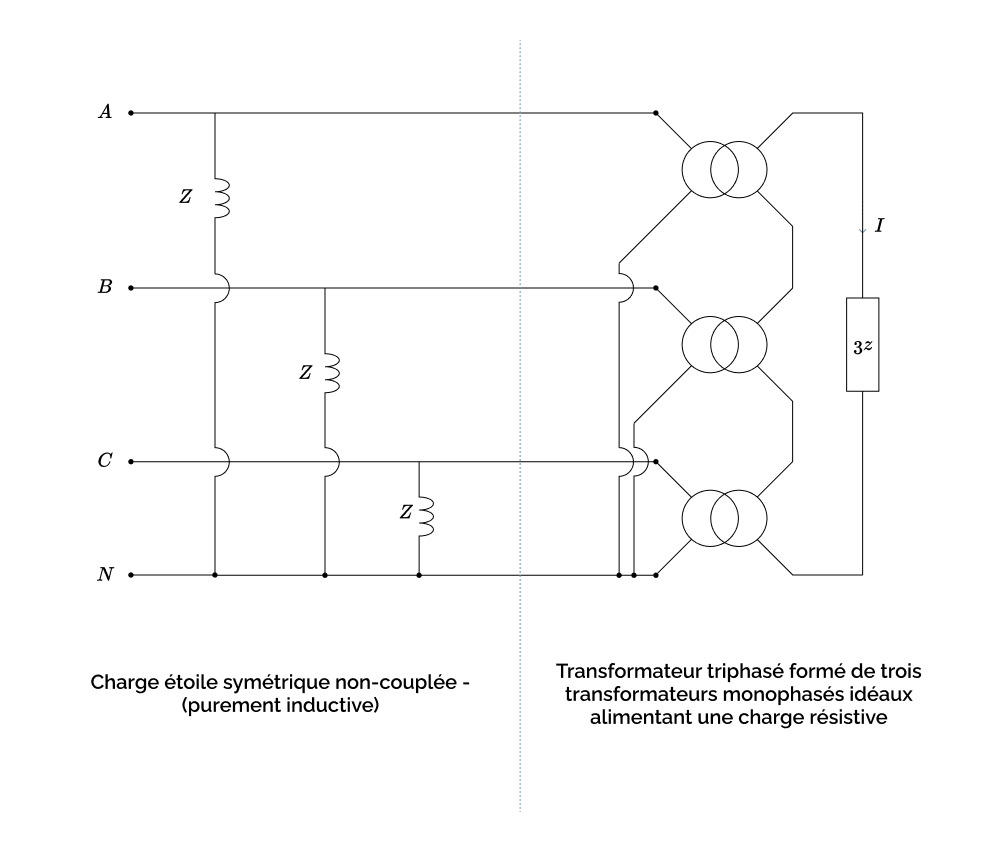
Les trois impédances magnétisantes placées au primaire forment une charge étoile purement inductive non-couplée classique, cas que nous avons déjà étudié cet article sur la charge étoile équilibrée. Celle-ci est placée en parallèle avec une charge plus exotique formée d’un assemblage de trois transformateurs monophasés qui alimentent une même charge \(3 z\) ; où \(z\) est l’inductance série, ramenée au secondaire, de chacun des trois transformateurs monophasés identiques.
On laisse de côté la charge étoile non-couplée formée par les trois inductances magnétisantes, et on se concentre sur la charge exotique dont les équations en coordonnées usuelles sont les suivantes :
\begin{equation}
\begin{cases}
I_A = I \\
I_B = I \\
I_C = I \\
V_A + V_B + V_C – 3 V_N = 3 z I \\
I_A + I_B + I_C + I_N = 0.
\end{cases}
\end{equation}
Ce modèle comporte 9 variables : 8 variables associées à ses 4 ports, et le courant \(I\) qui circule dans le triangle au secondaire et qui constitue une variable interne. Parmi ces 9 variables, on compte deux triplets triphasés \(V_{ABC}\) et \(I_{ABC}\), et trois variables isolées \(V_N\), \(I_N\) et \(I\).
Notre système d’équations comporte un bloc triphasé d’équations et deux équations isolées, soit 5 équations indépendantes. Le composant dispose donc de 4 degrés de liberté, comme on s’y attend pour un composant à 4 ports.
Les deux sous-matrices \(3 \times 3\) du bloc triphasé d’équations sont respectivement nulle (pour le triplet \(V_{ABC}\)) et égale à \(I_3\) (pour \(I_{ABC}\)) ; ces deux sous-matrices sont circulantes. La matrice \(A_1\) (au sens de l’équation 2.1) a deux colonnes nulles et une colonne égale à \( -\mathbf{1} \). Les matrices \(A^1\) et \(A^2\) ont chacune une ligne nulle et une ligne égale à \(\mathbf{1}^\top\). La matrice possède donc la structure circulante.
Enfin, toutes les matrices circulantes \(3 \times 3\) du problème vérifient \(\beta = \gamma \, (=0)\) au sens de la remarque 3 ; au vu de la remarque 17, on s’attend donc à ce que les système inverse et le système direct qui apparaîtront après le double changement de bases soient identiques.
Changement de base sur les triplets de variables triphasées
Effectuons le changement de variables habituel pour passer les deux triplets triphasés en coordonnées symétriques :
\begin{equation}
\label{eq:etoile-triangle-rien-post-Fortescue}
\begin{cases}
V_0 – V_N = z I \\
I_0 + I_i + I_d = I \\
I_0 + a I_i + a^2 I_d = I \\
I_0 + a^2 I_i + a I_d = I \\
3 I_0 + I_N = 0.
\end{cases}
\end{equation}
Changement de base sur les blocs triphasés d’équations
Effectuons maintenant le changement de base sur le bloc triphasé d’équations :
\begin{equation}
\begin{cases}
I_d = 0 \\
I_i = 0 \\
I_0 = I \\
V_0 – V_N = z I \\
3 I_0 + I_N = 0
\end{cases}
\end{equation}
que l’on peut reformuler
$$ V_0 – V_N = z I_0, \quad I_0 + \tilde{I}_N = 0, \quad I_d = 0 \quad \mbox{et} \quad I_i = 0 $$
et qui se découple bien en un système direct, un système inverse et un système homopolaire indépendants.
Schéma électrique symétrique
On peut interpréter notre charge de la manière suivante.
- dans le circuit direct, elle est équivalente à laisser en l’air le port \((V_d, I_d)\) : en effet, \(I_d\) est nul et \(V_d\) (qui n’apparaît pas dans les équations) est quelconque.
- De même, dans le circuit inverse, elle est équivalente à laisser en l’air le port \((V_i, I_i)\) : en effet, \(I_i\) est nul et \(V_i\) (qui n’apparaît pas dans les équations) est quelconque.
- Enfin, dans le circuit homopolaire, elle revient à placer une impédance \(z\) entre le port \((V_0, I_0)\) et le port \((V_N, \tilde{I}_N)\).
Le schéma électrique correspondant est présenté sur la figure ci-dessous :
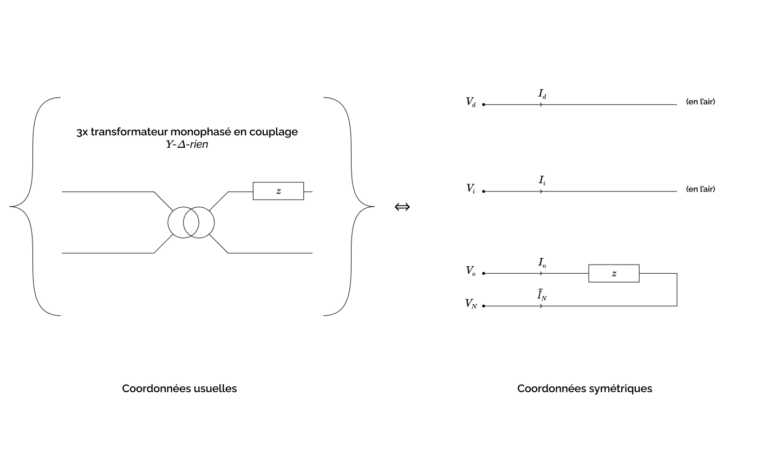
Remarque : L’impédance série \(z\) étant normalement très faible, on peut considérer cette charge comme un quasi-court-circuit homopolaire, associé à une impédance au contraire infinie (avant réintégration des impédances magnétisantes) en mode direct et en mode inverse. Ce composant sera donc transparent du point de vue direct et inverse, tandis qu’il appellera un courant homopolaire potentiellement énorme qui forcera la tension homopolaire \(V_0 – V_N\) à être quasi-nulle (voire nulle si on modélise le composant comme idéal en mettant \(z\) à zéro), sous réserve bien sûr que la source amont (homopolaire) soit modélisée comme non-idéale, de sorte que sa tension finira bien par s’effondrer si on tire suffisamment de courant. Inversement, si on modélise la source comme idéale et qu’on conserve un \(z\) non-nul dans la charge, alors la tension homopolaire restera inchangée et on aura simplement un courant gigantesque dans la charge ; et enfin, si on modélise les deux composants comme idéaux, alors le problème n’aura pas de solution.
Réintégration des inductances magnétisantes
Si, pour finir, on réintègre les équations de notre charge étoile purement inductive connectée en parallèle, en sommant les courants symétriques de nos deux objets, et après élimination de la variable interne \(I\), on aboutit pour notre équilibreur étoile-triangle-rien aux équations suivantes :
\begin{equation}
\begin{cases}
V_d = Z I_d \\
V_i = Z I_i \\
I_0 = (\frac{1}{z} + \frac{1}{Z}) (V_0 – V_N) \\
I_0 + \tilde{I}_N = 0.
\end{cases}
\end{equation}
La charge couplée étoile-triangle avec secondaire à vide est donc caractérisée simplement par les trois impédances symétriques suivantes :
$$ Z_d := Z, \quad Z_i := Z \quad \mbox{et} \quad Z_0 := \frac{z \cdot Z}{z + Z} \approx z, $$
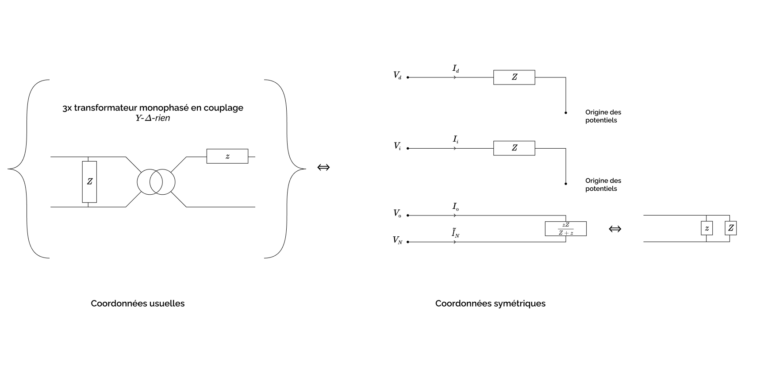
(où l’on rappelle que \(Z\) est l’impédance parallèle, dite magnétisante, de chacun des trois transformateurs monophasés identiques de rapport \(1\) qui constituent le dispositif, et \(z\) est leur impédance série). Ces impédances, comme dans les cas précédemment étudiés, s’entendent de la manière suivante : entre le port \((V_d, I_d)\) et l’origine des potentiels pour l’impédance directe, entre le port \((V_i, I_i)\) et l’origine des potentiels pour l’impédance inverse, et entre le port \((V_0, I_0)\) et le port \((V_N, \tilde{I}_N)\) pour l’impédance homopolaire. Le schéma électrique correspondant est présenté sur la figure ci-dessous :
