3.2.1 Ligne équilibrée simple à trois conducteurs
On considère une ligne composée de trois conducteurs identiques, chacun modélisé par une impédance propre \(Z\) et par une impédance mutuelle (soit \(j \omega\) fois l’inductance mutuelle) \(M\) avec chaque autre conducteur. On note de la façon habituelle les grandeurs associées à la première extrémité de la ligne, avec un prime les grandeurs associées à son autre extrémité.
Mise en équations en coordonnées usuelles
Les équations du système, sous forme matricielle par blocs, sont les suivantes :
\begin{equation}
\begin{cases}
V_{ABC} – V’_{ABC} = \mathcal{Z} \, I_{ABC}\\
I_{ABC} + I’_{ABC} = 0,
\end{cases}
\end{equation}
où
\( \mathcal{Z} =
\begin{bmatrix}
Z & M & M\\
M & Z & M\\
M & M & Z
\end{bmatrix}
.\)
Le problème comporte 12 variables qui forment 4 triplets de variables triphasées, sans aucune variable isolée, et qui sont toutes des variables de ports. Il comporte par ailleurs 6 équations indépendantes réparties en 2 blocs triphasés d’équations, sans aucune équation isolée. Le composant possède donc 6 degrés de liberté, comme on s’y attend pour un composant à 6 ports.
Les sous-matrices \(3 \times 3\) qui interviennent dans le système d’équations sont \(I_3\) et \(S\) qui sont toutes les deux des matrices circulantes. La matrice du problème possède donc la structure circulante.
Enfin, toutes les sous-matrices \(3 \times 3\) qui interviennent dans le problème vérifient \(\beta = \gamma\) au sens de la remarque 3 : on s’attend donc à ce que les schémas direct et inverse soient identiques.
Changement de base sur les triplets de variables triphasées
On effectue le changement de base directement par des calculs matriciels en utilisant la matrice de Fortescue \(F\) :
\begin{equation}
\begin{cases}
F \, V_{0id} – F \, V’_{0id} = \mathcal{Z} \, F \, I_{0id}\\
F \, I_{0id} + F \, I’_{0id} = 0.
\end{cases}
\end{equation}
Changement de base sur les blocs triphasés d’équations
On prémultiplie par \(F^{-1}\) pour obtenir :
\begin{equation}
\begin{cases}
V_{0id} – V’_{0id} = (F^{-1} \, \mathcal{Z} \, F) \, I_{0id}\\ I_{0id} + I’_{0id} = 0.
\end{cases}
\end{equation}
L’équation 1.7 nous donne
\(
F^{-1} \, \mathcal{Z} \, F =
\begin{bmatrix}
Z + 2 M & 0 & 0\\
0 & Z + (a + a^2) M & 0\\
0 & 0 & Z + (a + a^2) M
\end{bmatrix}
.\)
On peut rassembler ces équations en trois groupes ; un système direct
\begin{equation}
\begin{cases}
V_d – V’_d = (Z + (a + a^2) M) I_d \\
I_d + I_d’ = 0,
\end{cases}
\end{equation}
un système inverse
\begin{equation}
\begin{cases}
V_i – V’_i = (Z + (a + a^2) M) I_i \\
I_i + I_i’ = 0
\end{cases}
\end{equation}
et un système homopolaire
\begin{equation}
\begin{cases}
V_0 – V’_0 = (Z + 2 M) I_0 \\
I_0 + I_0′ = 0.
\end{cases}
\end{equation}
Les systèmes direct et inverse sont bien identiques, comme attendu.
Schéma électrique symétrique
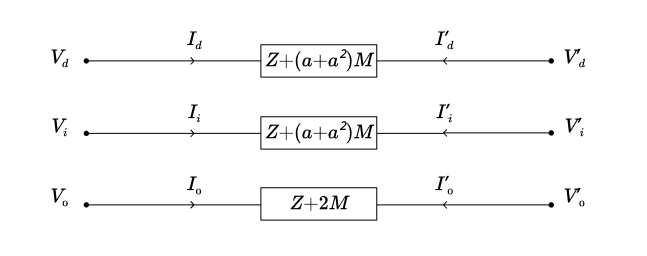
On peut interpréter ces trois systèmes d’équations découplés comme une impédance équivalente (dite « impédance cyclique ») de valeur \(Z + (a + a^2) M\) située entre les ports \((V_d, I_d)\) et \((V’_d, I’_d)\) ; une impédance de même valeur \(Z + (a + a^2) M\) située entre les ports \((V_i, I_i)\) et \((V’_i, I’_i)\) ; et une impédance de valeur \(Z + 2 M\) située entre les ports \((V_0, I_0)\) et \((V’_0, I’_0)\). Notre modèle de ligne simple, exprimé en coordonnées symétriques, est donc équivalent au schéma de la figure ci-dessous.
3.2.2 Ligne équilibrée simple à quatre conducteurs
On considère une ligne composée de trois conducteurs de phases identiques et d’un conducteur de neutre potentiellement différent. On introduit des impédances propres \(Z\) sur les phases et \(z\) sur le neutre, et des impédances mutuelles (soit \(j \omega\) fois l’inductance mutuelle) \(M\) entre chaque paire de conducteurs de phases, et \(m\) entre le neutre et une phase. On note de la façon habituelle les grandeurs associées à la première extrémité de la ligne, avec un prime les grandeurs associées à son autre extrémité.
Mise en équations en coordonnées usuelles
Les équations du système, sous forme matricielle par blocs, sont les suivantes :
\begin{equation}
\begin{cases}
V_{ABC} – V’_{ABC} = \mathcal{Z} \, I_{ABC} + m \, \mathbf{1} \, I_N \\
V_N – V’_N = m \, \mathbf{1}^\top I_{ABC} + z \, I_N\\
I_{ABC} + I’_{ABC} = 0 \\
I_N + I’_N = 0.
\end{cases}
\end{equation}
Le problème comporte 16 variables réparties en 4 triplets triphasés de variables et 4 variables isolées, et qui sont toutes des variables de ports. Il compte par ailleurs 8 équations réparties en 2 blocs triphasés d’équations et 2 équations isolées. Le composant possède donc 8 degrés de liberté, comme on s’y attend pour un composant à 8 ports.
Les sous-matrices \(3 \times 3\) qui apparaissent dans le système sont \(I_3\) et \(\mathcal{Z}\), qui sont circulantes. Dans le premier bloc triphasé d’équation, la sous-matrice associée à la variable isolée \(I_N\) est égale \(m \, \mathbf{1}\), et le deuxième bloc triphasé d’équation n’implique aucune variable isolée. Dans la première équation isolée, la ligne associée au triplet triphasé \(I_{ABC}\) est égale à \(m \, \mathbf{1}^\top\), tandis que la deuxième équation isolée ne fait intervenir aucun triplet triphasé. La matrice possède donc la structure circulante.
Enfin, toutes les sous-matrices \(3 \times 3\) qui interviennent dans le problème vérifient \(\beta = \gamma\) au sens de la remarque 3 : on s’attend donc à ce que les schémas direct et inverse soient identiques.
Changement de base sur les triplets de variables triphasées
On effectue le changement de variables, directement par des calculs matriciels :
\begin{equation}
\begin{cases}
F \, V_{0id} – F \, V’_{0id} = \mathcal{Z} \, F \, I_{0id} + m \, \mathbf{1} \, I_N \\
V_N – V’_N = m \, \mathbf{1}^\top F \, I_{0id} + z \, I_N\\
I_{0id} + I’_{0id} = 0 \\
I_N + I’_N = 0.
\end{cases}
\end{equation}
Changement de base sur le bloc triphasé d’équations
On prémultiplie le bloc triphasé d’équations par \(F^{-1}\) :
\begin{equation}
\begin{cases}
V_{0id} – V’_{0id} = F^{-1} \, \mathcal{Z} \, F \, I_{0id} + m \, F^{-1} \, \mathbf{1} \, I_N \\
V_N – V’_N = m \, \mathbf{1}^\top F \, I_{0id} + z \, I_N\\
I_{0id} + I’_{0id} = 0 \\
I_N + I’_N = 0.
\end{cases}
\end{equation}
Un petit calcul montre que \(F^{-1} \, \mathbf{1} = [1, 0, 0]^\top\), et que \(\mathbf{1}^\top F = [3, 0, 0]\) ; quant au calcul de \(F^{-1} \, \mathcal{Z} \, F\), il a été fait dans la section 3.2.1 précédente.
On aboutit à
\begin{equation}
\begin{cases}
V_d – V’_d = (Z + (a+a^2) M) I_d \\
V_i – V’_i = (Z + (a+a^2) M) I_i \\
V_0 – V’_0 = (Z + 2M) I_0 + m I_N \\
V_N – V’_N = 3 m I_0 + z \, I_N\\
I_{0id} + I’_{0id} = 0 \\
I_N + I’_N = 0
\end{cases}
\end{equation}
qui, pour ce qui concerne les systèmes direct et inverse, se décompose de la même manière que dans le cas d’une ligne à trois conducteurs, soit pour mémoire
\begin{equation}
\begin{cases}
V_d – V’_d = (Z + (a + a^2) M) I_d \\
I_d + I_d’ = 0,
\end{cases}
\end{equation}
pour le système direct, et
\begin{equation}
\begin{cases}
V_i – V’_i = (Z + (a + a^2) M) I_i \\
I_i + I_i’ = 0,
\end{cases}
\end{equation}
pour le système inverse ; tandis que pour le système homopolaire, on obtient
\begin{equation}
\begin{cases}
V_0 – V’_0 = (Z + 2M) I_0 + 3 m \tilde{I}_N \\
I_0 + I’_0 = 0 \\
V_N – V’_N = 3 m I_0 + 3 z \, \tilde{I}_N\\
\tilde{I}_N + \tilde{I}’_N = 0.
\end{cases}
\end{equation}
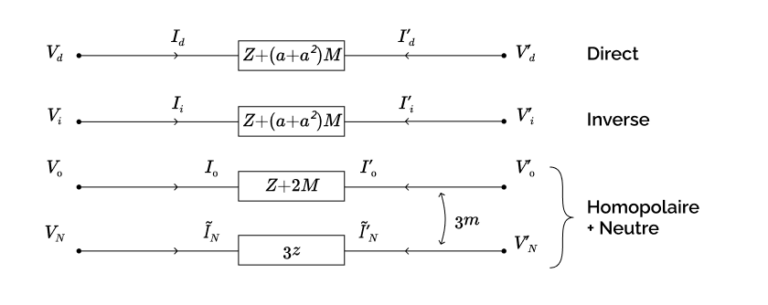
Schéma électrique symétrique
Le circuit équivalent est présenté sur la figure ci-dessous. On observe qu’il n’est pas tout à fait aussi simple que ceux que nous avons rencontrés jusqu’à présent : il reste ici une mutuelle entre le conducteur homopolaire et le conducteur de neutre.
3.2.3 Ligne équilibrée à trois conducteurs avec couplages capacitifs entre conducteurs
Ce cas peut être ramené à celui d’une charge (capacitive) en triangle équilibrée, suivie d’une ligne simple à trois conducteurs, suivie d’une autre charge (capacitive) en triangle équilibrée.3.2.4 Ligne équilibrée à quatre conducteurs avec couplages
capacitifs entre conducteurs
Ce cas peut être ramené à celui d’une charge (capacitive) en triangle équilibrée,
suivie d’une charge (capacitive) en étoile équilibrée à neutre relié, suivie
d’une ligne à quatre conducteurs, suivie d’une charge (capacitive) en étoile équilibrée à neutre relié, suivie d’une charge (capacitive) en triangle équilibrée.
3.2.5 Agrégation de lignes successives
Lorsque deux lignes sans éléments transversaux se succèdent, et qu’il n’y a pas de charge ni d’éléments shunts (entre conducteurs ou avec la terre) à leur point de connexion, ces lignes peuvent être agrégées par sommation de leurs impédances symétriques comme indiqué sur la figure ci-dessous, pour le cas d’une ligne à 3 conducteurs.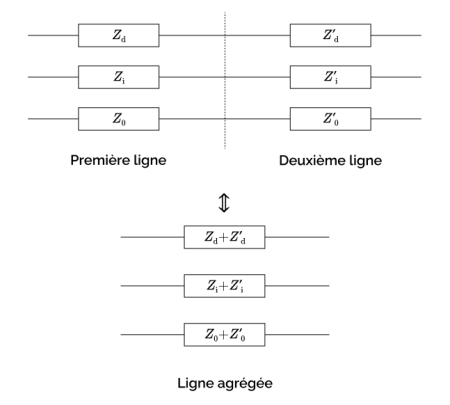
Sommaire
Partie 1 : Coordonnées usuelles et coordonnées symétriques
Partie 2 : Modélisation d’un composant triphasé équilibré passif général
Partie 3 : Modélisation symétrique des composants triphasés usuels
3.1.1 Charge étoile équilibrée
3.1.2 Charge triangle équilibrée
3.1.3 Cas d’une charge couplée équilibrée : le transformateur étoile-triangle avec secondaire à vide
3.2.1 Ligne équilibrée simple à trois conducteurs
3.2.2 Ligne équilibrée simple à quatre conducteurs
3.2.3 Ligne équilibrée à trois conducteurs avec couplages capacitifs entre conducteurs
3.2.4 Ligne équilibrée à quatre conducteurs avec couplages capacitifs entre conducteurs
3.2.5 Agrégation de lignes successives.
3.3 Transformateurs triphasés formés de trois transformateurs monophasés identiques
3.3.1 Transformateur étoile-étoile
3.3.2 Transformateur triangle-étoile
(travail en cours : publication prévue sur les mois de janvier à mars 2025)





