1.1 Un peu d’algèbre linéaire
1.1.1 Matrices circulantes
Une matrice circulante est une matrice carrée dans laquelle on passe d’une ligne à la suivante par décalage vers la droite des coefficients :
\begin{equation}
\begin{bmatrix}
c_0 & c_1 & c_2 & \dots & c_{n-1} \\
c_{n-1} & c_0 & c_1 & & c_{n-2} \\
c_{n-2} & c_{n-1} & c_0 & & c_{n-3} \\
\vdots & & & \ddots & \vdots \\
c_1 & c_2 & c_3 & \dots & c_0
\end{bmatrix}
\end{equation}
où les coefficients \(c_i\) sont des nombres complexes.
Cette structure de matrice joue un rôle fondamental dans la théorie des composantes symétriques, notamment en dimension \(3\) où une matrice circulante s’écrit plus simplement :
\begin{equation}
\label{eq:matrice-circulante-3×3}
\begin{bmatrix}
\alpha & \beta & \gamma \\
\gamma & \alpha & \beta \\
\beta & \gamma & \alpha
\end{bmatrix}
\end{equation}
avec \((\alpha, \beta, \gamma) \in \mathbb{C}^3\).
Soit
\begin{equation}
\label{eq:def-matrice-shift}
S :=
\begin{bmatrix}
0 & 1 & 0 \\
0 & 0 & 1 \\
1 & 0 & 0
\end{bmatrix}~;
\end{equation}
prémultiplier un vecteur (colonne) par \(S\) revient à décaler ses coordonnées vers le haut, tandis que postmultiplier un vecteur (ligne) par \(S\) revient à décaler ses coordonnées vers la droite. De même, prémultiplier une matrice \(3 \times 3\) par \(S\) revient à décaler ses lignes vers le haut, tandis que la postmultiplier par \(S\) revient à décaler ses colonnes vers la droite.
La matrice \(S^\top\) possède les propriétés opposées : prémultiplier une matrice \(3 \times 3\) par \(S^\top\) revient à décaler ses lignes vers le bas, tandis que la postmultiplier par \(S^\top\) revient à décaler ses colonnes vers la gauche. Ceci signifie notamment que (\(S\) est inversible et) \(S^{-1} = S^\top\).
Par définition, une matrice \(C \in \mathbb{C}^3\) est circulante si et seulement si elle vérifie
\begin{equation}
C S = S^\top C.
\end{equation}
La matrice \(S\) est elle-même une matrice circulante particulière.
1.1.2 Diagonalisation des matrices circulantes de taille 3
Dans toute la suite, on pose \(a := e^{j \frac{2 \pi}{3}}\).
On définit également \(\mathbf{1} := (1,1,1)^\top\).
On introduit la matrice de Fortescue :
\begin{equation}
\label{eq:F}
F :=
\begin{bmatrix}
1 & 1 & 1 \\
1 & a & a^2 \\
1 & a^2 & a
\end{bmatrix}
.
\end{equation}
Un petit calcul montre que \(F\) est inversible et que
\begin{equation}
\label{eq:inv_F}
F^{-1} = \frac{1}{3} F^{*}
\quad \quad
\left( = \frac{1}{3}
\begin{bmatrix}
1 & 1 & 1 \\
1 & a^2 & a \\
1 & a & a^2
\end{bmatrix}
\right)
\end{equation}
où \(F^{*}\) désigne la conjuguée de \(F\).
Soit \(C\) une matrice circulante de taille 3, de la forme indiquée à l’équation (2). Un autre petit calcul montre que
\begin{equation}
\label{eq:F-diagonalise-C}
F^{-1} C F =
\begin{bmatrix}
\alpha + \beta + \gamma & 0 & 0 \\
0 & \alpha + a \beta + a^2 \gamma & 0 \\
0 & 0 & \alpha + a^2 \beta + a \gamma
\end{bmatrix},
\end{equation}
autrement dit que la matrice \(F\) diagonalise la matrice \(C\).
Remarque :
La matrice \(F\) ne dépend pas des valeurs de \(\alpha\), \(\beta\) et \(\gamma\) : elle diagonalise toutes les matrices circulantes de taille 3. Les paramètres \(\alpha\), \(\beta\) et \(\gamma\) n’interviennent que dans les valeurs propres, pas dans les vecteurs propres. Lorsque, dans la suite de ce document, nous serons amenés à diagonaliser de nombreuses matrices circulantes différentes, les équations de changement de base seront donc toujours les mêmes.
Remarque :
Les trois valeurs propres sont l’image par \(F\) du vecteur \([\alpha, \beta, \gamma]^\top\).
Remarque :
La deuxième ligne et la troisième ligne sont la conjuguée l’une de l’autre. De plus, si \(\beta = \gamma\), alors la deuxième ligne et la troisième ligne sont réelles et égales.
En notant \(X’\) les coordonnées dans la base de Fortescue d’un vecteur \(X\), les relations de passage s’écrivent
$$ X = F \, X’, \quad X’ = F^{-1} \, X. $$
On note
\begin{equation}
X’ :=
\begin{bmatrix}
X_0 \\
X_{i} \\
X_{d}
\end{bmatrix}
\end{equation}
et l’on nomme sa première coordonnée la composante homopolaire, la deuxième sa composante inverse, et la troisième sa composante directe. Nous désignerons la nouvelle base sous le nom de « base de Fortescue ».
Remarque :
L’ordre des trois coordonnées dans la nouvelle base est arbitraire ; on aurait pu faire un choix différent, ce qui aurait mené à des matrices \(F\) et \(F^{-1}\) différentes. Il est simplement souhaitable de fixer cet ordre une fois pour toutes, afin de ne pas risquer de se tromper lorsqu’on fait des calculs matriciels. L’humanité ne semble malheureusement pas y être parvenue : si tout le monde s’accorde apparemment à placer la composante homopolaire en première position, on trouve en revanche dans la littérature les deux ordres possibles (direct puis inverse, et inverse puis direct) pour les deux variables restantes. Dans ce document, nous adopterons l’ordre suivant : homopolaire, inverse, direct.
1.2 Coordonnées symétriques dans les réseaux électriques triphasés
1.2.1 Définition et interprétation
Dans le contexte de l’étude d’un problème de réseau électrique, le « passage en coordonnées symétriques » consiste à représenter les grandeurs triphasées du problème non pas dans la base canonique, mais dans la base de Fortescue.
Autrement dit, cela consiste à décrire un triplet, disons, de courants (\(I_A\), \(I_B\), \(I_C\)) non plus comme la somme, ou « superposition » dans le langage des électrotechniciens, des trois courants
$$ I_A \times
\begin{bmatrix}
1 \\
0 \\
0
\end{bmatrix},
\quad
I_B \times
\begin{bmatrix}
0 \\
1 \\
0
\end{bmatrix},
\quad
\mbox{et }
I_C \times
\begin{bmatrix}
0 \\
0 \\
1
\end{bmatrix}
$$
comme on le fait quand on utilise la base canonique, mais comme la superposition des trois courants
$$ I_0 \times
\begin{bmatrix}
1 \\
1 \\
1
\end{bmatrix},
\quad
I_i \times
\begin{bmatrix}
1 \\
a \\
a^2
\end{bmatrix},
\quad
\mbox{et }
I_d \times
\begin{bmatrix}
1 \\
a^2 \\
a
\end{bmatrix}.
$$
Le troisième de ces vecteurs,
$$\begin{bmatrix}
I_d \\
a^2 I_d \\
a I_d
\end{bmatrix}
$$
est triphasé équilibré direct. La coordonnée correspondante, appelée « le courant direct \(I_d\) » peut être interprétée comme la composante directe du courant sur la phase A, tandis que la composante directe du courant sur la phase B est égale à \(a^2 I_d\) (rotation de \(I_d\) d’un angle \(-\frac{2\pi}{3}\)) et que la composante directe du courant sur la phase C est égale à \(a I_d\) (rotation de \(I_d\) d’un angle \(\frac{2\pi}{3}\)).
Le deuxième de ces vecteurs,
$$\begin{bmatrix}
I_i \\
a I_i \\
a^2 I_i
\end{bmatrix}
$$
est triphasé équilibré inverse. De même, le « courant inverse \(I_i\) » peut être interprété comme la composante inverse du courant sur la phase A, tandis que la composante inverse du courant sur la phase B est égale à \(a I_i\) et que la composante inverse du courant sur la phase C est égale à \(a^2 I_i\).
Remarque :
Le fait que la théorie des composantes symétriques singularise la phase A aura des conséquences pratiques dans les calculs ; ainsi par exemple, dans le cas du défaut biphasé-terre que nous étudierons plus loin dans ce document, les calculs seront plus simples et plus élégants si le défaut est placé entre les phases B et C que s’il est placé, par exemple, entre les phases A et B. Cette situation ne se produit pas lorsqu’on reste en coordonnées usuelles : les calculs à réaliser sont alors essentiellement les mêmes, quelle que soit la paire de phase à laquelle on applique le défaut.
Enfin, le premier de ces vecteurs,
$$\begin{bmatrix}
I_0 \\
I_0 \\
I_0
\end{bmatrix}
$$
est triphasé équilibré « homopolaire », ce qui signifie par définition que toutes ses coordonnées sont égales. Le « courant homopolaire \(I_0\) » peut donc être interprété comme la composante homopolaire du courant sur chacune des phases.
La même logique s’applique pour un triplet triphasé de potentiels (\(V_A\), \(V_B\), \(V_C\)), que la représentation en composantes symétriques consiste à décrire comme la superposition, premièrement d’un triplet direct
$$
\begin{bmatrix}
V_d \\
a^2 V_d \\
a V_d
\end{bmatrix}
$$
où \(V_d\) représente la composante directe du potentiel sur la phase A, et où les potentiels sur les phases B et C s’en déduisent par rotation (c’est-à-dire par multiplication par \(a^2\) et \(a\) respectivement) ; deuxièmement, d’un triplet inverse
$$
\begin{bmatrix}
V_i \\
a V_i \\
a^2 V_d
\end{bmatrix}
$$
où \(V_i\) représente la composante inverse du potentiel sur la phase A, et où les potentiels sur les phases B et C s’en déduisent par rotation (c’est-à-dire par multiplication par \(a\) et \(a^2\) respectivement) ; et enfin troisièmement d’un triplet homopolaire
$$
\begin{bmatrix}
V_0 \\
V_0 \\
V_0
\end{bmatrix}
$$
où \(V_0\) représente le potentiel, identique, sur chacune des phases.
Autrement dit, au lieu de représenter une grandeur triphasée en donnant sa valeur sur les trois phases (\(X_A = \dots\), \(X_B = \dots\), \(X_C = \dots\)), on la représente en donnant les composantes directe, inverse et homopolaire de la grandeur pour phase A uniquement (\(X_A = X_0 + X_i + X_d\)), ce qui est suffisant puisque les composantes de la grandeur sur les autres phases s’en déduisent sans ambiguïté, par rotation (pour les composantes directe et inverse) ou par égalité (pour la composante homopolaire).
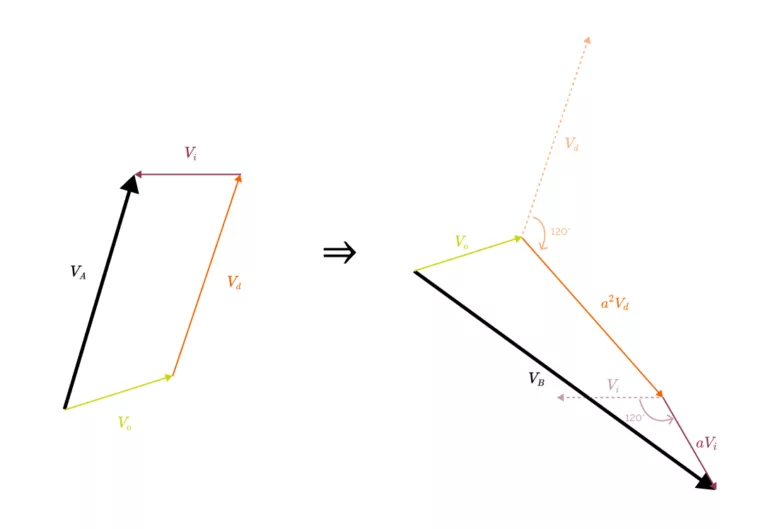
1.2.2 Propriétés
1.2.2.1 Transformée de vecteurs particuliers
Soit \(X\) un vecteur triphasé équilibré direct ; on a \(X_B = a^2 X_A\) et \(X_C = a X_A\), et les coordonnées symétriques de \(X\) sont donc
\begin{equation}
\label{eq:comp_sym_TED}
X_0 = 0, \quad X_i = 0, \quad X_d = X_A.
\end{equation}
De même pour un système triphasé équilibré indirect (\(X\), \(a X\), \(a^2 X\)), on aurait
\begin{equation}
X_0 = 0, \quad X_i = X, \quad X_d = 0.
\end{equation}
et pour un système homopolaire (\(X\), \(X\), \(X\)) on aurait
\begin{equation}
X_0 = X, \quad X_i = 0, \quad X_d = 0.
\end{equation}
La première colonne de \(F^{-1}\) étant égale à \(\frac{1}{3} \mathbf{1}\), on peut aussi noter qu’une grandeur purement monophasée et placée sur la phase A est « 1/3 directe, 1/3 inverse et 1/3 homopolaire ».
Remarque :
Cette propriété ne s’applique pas une grandeur purement monophasée placée sur la phase B ou sur la phase C. On retrouve le fait que le passage en composantes symétriques singularise la phase A.
1.2.2.2 Quasi-conservation de la puissance
La puissance entrante dans un triplet triphasé de ports (\(V\), \(I\)) \(\in \mathbb{C}^3 \times \mathbb{C}^3\) est :
$$ S = V^T I^* = (V’)^\top (F^\top F^*) (I’)^* = 3 (V’)^T (I’)^*. $$
Remarque :
La puissance transmise sur un conducteur est définie comme le produit du potentiel et du courant conjugué, et la puissance transmise par un ensemble de conducteurs est définie comme la somme des puissances transmises sur chaque conducteur. Il faut donc garder en tête que la puissance transmise sur un conducteur dépend de l’origine choisie pour les potentiels, et que la puissance transmise par un ensemble de conducteurs en dépend a priori aussi, sauf dans le cas usuel où la somme des courants sur l’ensemble des conducteurs considérés est nul ; on montre alors facilement que le choix de l’origine des potentiels n’a plus d’importance. Or, dans le contexte de la théorie des composantes symétriques, on étudie fréquemment des situations de défaut et notamment de défauts à la terre, pour lesquels la somme des courants sur les trois phases n’est pas nulle. On doit donc être extrêmement prudent quand on parle de la puissance transmise par une ligne dans une telle situation, car cette valeur n’a guère de sens physique : elle dépend de l’origine, arbitraire, des potentiels.
En introduisant les puissances symétriques
$$ S_0 := V_0 I_0^*, \quad S_{i} := V_{i} I_{i}^*, \quad \mbox{et } S_{d} := V_{d} I_{d}^*, $$
on a donc
$$ S = 3 (S_0 + S_{i} + S_{d}). $$
Il n’y a donc pas littéralement conservation de la puissance lorsqu’on passe en composantes symétriques (il faut penser à ajouter le facteur \(3\)), mais presque.
Ce facteur \(3\) est en fait assez naturel : souvenons-nous, en effet que la modélisation en composante symétrique « ne représente que la phase A », et non pas l’ensemble des trois phases ; on n’est donc guère surpris d’apprendre que la puissance que l’on a calculée en coordonnées symétriques doit être multipliée par \(3\) pour revenir à la puissance au sens usuel.
Remarque :
Si l’on avait défini \(F\) en la divisant par \(\sqrt{3}\) (disons \(G := \frac{F}{\sqrt{3}}\)), on aurait même \(G^{-1} = G^{(\top,*)}\) et la matrice serait donc unitaire (1) (elle conserverait le produit scalaire hermitien, donc la puissance complexe). C’est sans doute le choix qui aurait été fait par un mathématicien ; mais la définition de \(F\) que nous avons donnée présente l’avantage de donner une interprétation simple aux grandeurs symétriques (« ça représente ce qui se passe sur la phase A »), ce qui est assez agréable aussi.
1.2.2.3 Invariance par translation des composantes directe et inverse de la tension
Puisque \(1 + a + a^2 = 0\), les composantes inverse et directe d’un triplet triphasé sont invariantes lorsque le jeu de trois vecteurs d’origine subit une translation. On sent donc qu’on peut donc les déterminer uniquement à partir de la connaissance de la forme du triangle que constitue dans le plan complexe le triplet triphasé considéré, sans connaître la position absolue de ce triangle ; autrement dit, on sent que les composantes inverse et directe peuvent être déterminées à partir de la connaissance des tensions composées uniquement, sans avoir la connaissance des tensions simples. C’est effectivement le cas, car
$$ X_{i} := \frac{1}{3} (X_1 + a^2 X_2 + a X_3) = \frac{1}{3} (a^2 (X_2 – X_1) + a (X_3 – X_1)) $$
et
$$ X_{d} := \frac{1}{3} (X_1 + a X_2 + a^2 X_3) = \frac{1}{3} (a (X_2 – X_1) + a^2 (X_3 – X_1)). $$
Remarque :
Cette propriété est particulièrement importante dans le cas où l’on considère un triplet triphasé de potentiels : elle signifie en effet notamment que ses composantes directe et inverse ne dépendent pas de l’origine, arbitrairement choisie, des potentiels. Une première conséquence de cette observation est que l’on peut sans rougir s’autoriser à parler, comme le font habituellement les électrotechniciens, de la tension directe \(V_d\) et de la tension inverse \(V_i\). En effet, la situation est analogue à celle d’une tension au sens usuel, qui est indépendante du choix de l’origine des potentiels parce qu’elle consiste en une combinaison linéaire de (deux) potentiels dont les coefficients, \([1, -1]\), sont à somme nulle ; c’est à peu près la même chose pour les tensions directe et inverse (2), avec une combinaison linéaire à somme nulle de (trois) potentiels avec les coefficients \([1, a, a^2]\). Une deuxième conséquence est qu’en pratique, les tensions directe et inverse sont accessibles à la mesure sans ambiguïté en tout point du réseau, à l’origine des phases près (c’est-à-dire à une rotation près dans le plan complexe) : on peut donc notamment utiliser tout indicateur construit à partir des tensions inverse et/ou directe (du moins tout indicateur invariant par rotation de ces tensions dans le plan complexe), comme critère de déclenchement dans un relais de protection. La norme de la tension directe et de la tension inverse, notamment, sont indépendantes de l’origine des phases, et constituent donc des indicateurs bien définis, de même que leur ratio \(\frac{|V_i|}{|V_d|}\) que l’on nomme le « facteur de déséquilibre » et qui est parfois utilisé pour quantifier le degré de déséquilibre en tension d’un système triphasé.
Remarque :
A contrario, la « tension homopolaire » \(V_0\), que je préférerais appeler le « potentiel homopolaire » comme indiqué précédemment, est une grandeur non-physique, au sens où elle dépend de l’origine arbitraire des potentiels et n’est donc pas mesurable. Ce qui a bien du sens physique, et que l’on peut mesurer, c’est la différence entre \(V_0\) et un autre potentiel ; en pratique, il s’agit généralement :
- soit de celui du conducteur de neutre (quand il existe), ou simplement d’un point neutre (d’une charge, d’un transformateur),
- soit celui de la terre.
En effet, on revient alors à une combinaison linéaire de (quatre) potentiels avec des coefficients (\(\frac{1}{3}\), \(\frac{1}{3}\), \(\frac{1}{3}\), \(-1\)) dont la somme est nulle ; le résultat est donc bien quelque chose d’indépendant de l’origine des potentiels, et qui mérite le nom de « tension ».
Lorsque l’on utilise en pratique la tension homopolaire comme critère de détection dans les relais de protection, c’est en fait de la différence de potentiel \(V_0 – V_G\) (où \(V_G\) est le potentiel de la terre locale) que l’on parle. Cette grandeur est bien mesurable… et dépend du potentiel de la terre locale, pas uniquement de ce qui se passe sur le réseau électrique lui-même, ce qui est paradoxal pour une protection dont le but est de détecter un problème sur le réseau (3)! Mais comme les électrotechniciens considèrent généralement le potentiel de la terre comme égal en tout point, et fixé à \(0\), ils ne s’en préoccupent pas et assimilent le potentiel homopolaire \(V_0\) à quelque chose de mesurable (du moment qu’on dispose d’un piquet de terre).
On retient donc que les tensions directe et inverse, au même titre que les tensions composées, donnent la forme du triangle des potentiels au sens usuel, forme qui est indépendante de l’origine des potentiels ; tandis que le potentiel homopolaire donne la position (du centre de gravité) de ce triangle, par rapport à une certaine origine arbitraire et n’a donc pas de sens physique en lui-même. Ce potentiel homopolaire ne mérite donc pas le nom de homopolaire que lui donnent souvent les électrotechniciens. La différence entre la position de ce centre de gravité et celle du potentiel de neutre, ou de terre, ou autre, est en revanche physiquement significative, et mérite bien d’être appelée la tension homopolaire ; mais il faut alors garder en tête que l’appellation est ambiguë, parce qu’elle ne dit pas avec quel point on effectue le calcul de différence de potentiel. Il serait donc plus clair, et plus rigoureux, de parler non pas de « tension homopolaire » mais de tension « homopolaire-neutre » ou tension « homopolaire – terre locale », ou à la rigueur de tension « homopolaire – terre » (charge au lecteur de savoir s’il s’agit de la terre locale ou si cela n’a pas d’importance parce que l’on suppose que le potentiel de la terre est le même partout).
Exemple : considérons une source de tension triphasée idéale alimentant une charge impédante en étoile à neutre non-relié. Quel que soit le potentiel du point neutre de la charge, le potentiel des trois phases restera celui de la source idéale de tension. Les composantes directe et inverse du triplet des tensions simples par rapport au point neutre de la charge seront donc les mêmes qu’au niveau de la source. En particulier, si la source est triphasée équilibrée directe, alors la composante inverse de la tension mesurée à partir du point neutre de la charge sera toujours nulle, aussi déséquilibrée que soit la charge impédante.
1.3 Schémas électriques symétriques
1.3.1 Interprétation électrique des équations symétriques
Lorsqu’on travaille en coordonnées usuelles, on peut se représenter le problème soit sous forme d’équations, soit de manière équivalente sous forme d’un circuit électrique. Ces représentations sont complémentaires, et souvent toutes deux utiles ; la représentation sous forme de circuit permet notamment de faire apparaître clairement certaines possibilités de simplifications, comme le fait de regrouper des impédances placées en série ou en parallèle, qui sautent beaucoup moins aux yeux quand on travaille directement sur un système d’équations.
Le passage en coordonnées symétriques produit un jeu d’équations nouveau ; celui-ci peut-il aussi être interprété comme un schéma électrique, ce qui permettrait de conserver la même double représentation qu’en coordonnées usuelles ?
Il semblerait que oui ! En tout cas, au prix d’un petit changement de variable supplémentaire qui sera présenté dans la section 1.4 suivante, c’est le cas pour tous les composants que nous allons traiter dans ce document. Pour chacun, nous présenterons donc à la fois un modèle sous forme d’équations écrites dans la base de Fortescue, et un schéma électrique équivalent faisant intervenir les variables associées à la nouvelle base.
1.3.2 Cas particulier du conducteur de neutre
La représentation en composantes symétriques revient essentiellement à ne décrire que ce qui se passe sur la phase A, sous une forme qui permet de déduire sans ambiguïté se qui se passe sur les deux autres phases. Le courant homopolaire \(I_0\), notamment, représente le courant homopolaire sur la phase A (et il se trouve que le même courant circule sur les phases B et C). Le courant \(I_N\), lui, représente le courant qui revient par le neutre et qui, généralement, sera égal à la somme des courants sur les trois phases soit \(3 I_0\). Dans ces conditions, il ne sera souvent pas possible de se représenter sous forme d’un circuit électrique (simple, du moins) les équations impliquant à la fois \(I_0\) et \(I_N\) ; typiquement, on ne pourra pas le faire sous la forme d’une simple impédance placée entre un « port homopolaire » (\(V_0\), \(I_0\)) et le port de neutre (\(V_N\), \(I_N\)), à cause du facteur \(3\) indésirable.
La solution préconisée par l’auteur est d’effectuer systématiquement, lorsqu’on passe en coordonnées symétriques, le changement de variable trivial
\begin{equation}
I_N \longrightarrow \tilde{I}_N := \frac{I_N}{3}
\end{equation}
et d’introduire dans le problème le port (\(V_N\), \(\tilde{I}_N\)) en substitution au port (\(V_N\), \(I_N\)). Cette manipulation permet de conserver l’idée que l’on représente « uniquement ce qui se passe sur la phase A », y compris en ce qui concerne le conducteur de neutre dont on ne représentera que la fraction du courant, \(\tilde{I}_N\), qui est apportée par la phase A. Elle sera appliquée à tous les composants qui utilisent le port neutre, c’est-à-dire non seulement à ceux qui possèdent eux-mêmes un port neutre (par exemple, une charge étoile à neutre sorti) mais aussi à ceux que l’on relie au port neutre d’un autre composant. Cette dernière situation sera notamment celle du composant « terre », si celle-ci est modélisée de façon non-triviale avec des impédances, et non pas simplement assimilée à un noeud unique. Les impédances de ces conducteurs auxiliaires (neutre, terre, mises à la terre) seront donc multipliées par \(3\) dans les schémas faisant intervenir \(\tilde{I}_N\) par rapport à ceux faisant intervenir \(I_N\).
1.4 Noeuds
Le passage en coordonnées symétriques fait disparaître les variables de port, dont nous avons pourtant grandement besoin puisque ce sont elles qui permettent de relier les composants les uns aux autres via les équations des ports : égalité des potentiel des ports reliés à un même noeud, et nullité de la somme des courants entrant ou sortant du noeud. Nous allons voir dans cette partie différentes manières de résoudre ce problème.
1.4.1 Conservation des coordonnées usuelles pour les équations de noeuds
Il est tout à fait possible de n’utiliser les coordonnées symétriques que pour exprimer les équations internes d’un composant, et de conserver les coordonnées usuelles pour les équations de port. Ceci nécessite de conserver dans le problème à la fois les variables usuelles et les variables symétriques, et d’ajouter les relations de passage aux équations du problème ; cette approche n’est donc pas très élégante, ni très compacte, et lorsque tous les composants d’un problème sont décrits par leurs équations en coordonnées symétriques, on lui préférera certainement l’approche décrite dans la partie 1.5 ci-dessous et qui consiste à passer les équations de ports en coordonnées symétriques.
Cependant, on peut aussi légitimement ne souhaiter modéliser que certains composants en coordonnées symétriques, et en conserver d’autres en coordonnées usuelles : en effet,
- de façon générale, il nous semble préférable d’exprimer les équations des composants et celles des ports en coordonnées usuelles lorsqu’on étudie des systèmes triphasés généraux (4); cela rend les modèles plus facilement compréhensibles, ce qui évite les risques d’erreurs de modélisation et, dans le cas d’une implémentation informatique, rend le code plus maintenable. C’est en tout cas ce qui ressortira du chapitre 6.
- Cependant, dans le cas particuliers des composants triphasés équilibrés complexes, c’est plutôt l’inverse : ces composants sont décrits de façon plus élégante en coordonnées symétriques qu’en coordonnées usuelles. C’est notamment le cas des transformateurs triphasés, pour lesquels on peut proposer un modèle symétrique simple, élégant, compact et unifié, applicable à tous les couplages à l’exception du cas un peu particulier du transformateur étoile-étoile, et à la fois aux transformateurs à flux libre et à ceux à flux forcé ; tandis que leur modélisation en coordonnées usuelles est beaucoup plus laborieuse. Pour les composants équilibrés complexes, c’est donc plutôt en restant en coordonnées usuelles que l’on aboutit à des modèles verbeux qui augmentent le risque d’erreur et nuisent à la maintenabilité du code informatique.
Ainsi, lorsqu’on analyse des systèmes constitués de composants triphasés généraux, dont certains sont équilibrés (transformateurs, lignes…) mais pas tous (charges, défauts…), il ne semble pas déraisonnable de mélanger d’une part des modèles symétriques, pour les composants triphasés complexes ; et d’autre part des modèles usuels, pour les composants déséquilibrés et pour les composants équilibrés simples (5). Dans ce cas de figure, on pourra conserver les équations de ports en coordonnées usuelles.
1.4.2 Passage des équations de ports en coordonnées symétriques
1.4.2.1 Couplage de ports isolés
Considérons un noeud auquel sont connectés \(n\) ports (\(V_i\), \(I_i\)), \(i \in \{1, \dots n\}\). Ces ports sont supposés isolés, c’est-à-dire n’appartenant pas à un triplet triphasé de ports ; il s’agira typiquement des ports de neutre des composants qui possèdent un point neutre, ou du port de terre des composants qui possèdent un couplage avec la terre. Les variables (\(V_i\), \(I_i\)) sont donc des variables isolées et ne sont donc pas concernées par le changement de base que l’on opérera sur les triplets de variables triphasées pour passer le problème en coordonnées symétriques. Les équations d’un tel noeud seront conservées sans le moindre changement lors changement de base et resteront donc :
$$ V_i = V_1, \, \forall i \in \{2, \dots n\} \quad \mbox{et} \quad \sum_{i=1}^n I_i = 0. $$
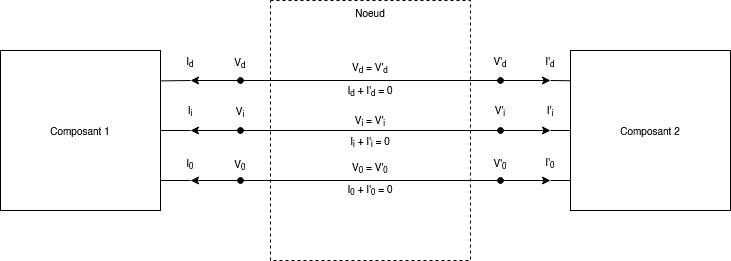
1.4.2.2 Couplage naturel de triplets de ports triphasés
Considérons maintenant trois noeuds auquel sont connectés \(n\) triplets de ports (\(V^{ABC}_i\), \(I^{ABC}_i\)), \(i \in \{1, \dots n\}\). On suppose que tous les ports qui appartiennent à la phase A sont connectés entre eux, et ainsi de suite pour les phases B et C. En coordonnées usuelles, les équations du triplet de noeuds sont :
$$ V^{ABC}_i = V^{ABC}_1, \, \forall i \in \{2, \dots n\} \quad \mbox{et} \quad \sum_{i=1}^n I^{ABC}_i = 0. $$
Le changement de variables s’écrit alors simplement :
$$ V^{0id}_i = V^{0id}_1, \, \forall i \in \{2, \dots n\} \quad \mbox{et} \quad \sum_{i=1}^n I^{0id}_i = 0~; $$
autrement dit, tout se passe comme si nous disposions maintenant d’un triplet de ports « homopolaire, inverse, direct » en lieu et place du triplet de ports « A, B, C ».
On peut donc coupler entre eux les composants représentés par des modèles en coordonnées symétriques, exactement de la même manière que l’on couple des composants entre eux en coordonnées usuelles : les équations seront les mêmes (égalité des potentiels symétriques, nullité de la somme des courants symétriques), et on représentera donc ces équations graphiquement par les mêmes schémas, comme illustré dans la figure ci-dessous :
1.4.3 Couplages contre-nature
Nous venons d’étudier les cas habituels que sont premièrement le couplage de ports isolés entre eux, et deuxièmement le couplage de triplets de ports triphasés entre eux en respectant l’identité des phases : on couple les ports de la phase A entre eux, les ports de la phase B entre eux, et ceux de la phase C entre eux.
On peut également concevoir des couplages plus inhabituels, comme enchaîner deux lignes en croisant les conducteurs (la phase A de la sortie de la première ligne est connectée à la phase B de l’entrée de la deuxième…), mélanger les phases et le neutre (alimenter une charge triangle entre la phase A, la phase B et le neutre du réseau…), voire pire (raccorder le port A du composant 1 au port A du composant 2, le port B du composant 1 au port B du composant 3…).
Si l’on rencontre ce genre de cas pathologique, l’écriture des équations de ports en coordonnées usuelles et leur changement de base doivent être réalisés au cas par cas. Cette situation se produit par exemple si l’on modélise un équilibreur zig-zag à partir de trois transformateurs monophasés indépendants. Les deux ports du primaire (respectivement du secondaire) de chaque transformateur monophasé sont alors connectés à deux noeuds triphasés différents : l’un au noeud triphasé de connexion avec le réseau amont, et l’autre à un noeud triphasé interne au composant.
1.5 Construction géométrique des composantes symétriques
Il existe des méthode de construction géométrique dans le plan complexe des composantes symétriques d’un triplet de complexes. Elles sont peut-être occasionnellement utiles, lorsqu’on souhaite analyser un problème de façon visuelle dans le diagramme de Fresnel en complément de l’approche classique basée sur des calculs d’algèbre linéaire dans \(\mathbb{C}\). Nous ne prendrons néanmoins pas le temps de les exposer ici, et ne nous en servirons pas dans la suite de ce document.
Notes
1. On a observé qu’une matrice circulante \(C\) de taille \(3\) était diagonalisable en base orthonormée, celle des colonnes de la matrice \(G\) définie dans la remarque précédente, mais avec des valeurs propres complexes. Le fait que \(C\) ne soit pas hermitienne (elle n’est pas nécessairement égale à sa transconjuguée) ne contredit donc pas le théorème selon lequel une matrice est hermitienne si et seulement si elle est diagonalisable en base orthonormée avec des valeurs propres réelles. Autrement dit, si \(C\) était diagonalisable en base orthonormée avec \(D\) réelle, alors on aurait \(C = G^{-1} D G = G^{(\top,*)} D G\) et donc \(C^{(\top,*)} = G^{(\top,*)} D^{(\top,*)} G = G^{(\top,*)} D G = C\). Ce cas se produit si et seulement si \(\beta = \gamma^*\) dans l’équation (\ref{eq:matrice-circulante-3×3}) : dans ce cas, \(C\) devient hermitienne et \(D\) devient réelle.
2. A contrario, la notion de « tension homopolaire » semble nettement plus discutable, mais elle est très ancrée dans le vocabulaire usuel. Le terme de « potentiel homopolaire » semble préférable, pour rappeler que cette grandeur dépend du choix arbitraire de l’origine des potentiels. Le terme de « tension homopolaire » pourrait en revanche être légitimement appliqué à l’expression \(V_0 – V_N\), pour les composants qui possèdent un point neutre.
3. Pour le dire autrement, si le potentiel de la terre locale variait pour une raison qui n’a rien à voir avec le réseau que l’on cherche à protéger, la protection déclencherait de façon intempestive.
4. Par opposition d’une part aux systèmes composés uniquement de composants équilibrés, pour lesquels le passage en coordonnées symétriques est élégant, compact et possède une jolie propriété de découplage~; et d’autre part aux systèmes en situation de défaut, qui n’entrent généralement pas dans la catégorie précédente mais qui font traditionnellement l’objet d’approximations drastiques (on néglige les charges) qui permettent parfois, comme pour le traitement du défaut-biphasé terre par la méthode des schémas électriques symétriques, de conduire les calculs de façon plus élégante en coordonnées symétriques qu’en coordonnées usuelles.
5. Une charge étoile équilibrée, par exemple peut être décrite de façon très simple dans les deux systèmes de coordonnées ; autant, donc, le faire en coordonnées usuelles, ce qui permet du point de vue informatique d’utiliser un même modèle pour les charges étoile équilibrées et pour les charges étoile déséquilibrées
